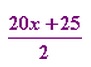In
this lesson, you will be able to perform multiplying rational algebraic
expressions. But before that, let’s look back on the concepts
that you have learned that are essential to this lesson.
To multiply fractions, we multiply the numerators together, multiply the denominators together, and then simplify. If necessary, we may use the rule
With regular fractions, multiplying and dividing is fairly simple, and is much easier than adding and subtracting. The situation is much the same with rational expressions (that is, with polynomial fractions).
Remember how you multiply regular fractions: You multiply across the top and bottom. For instance:
And you need to simplify, whenever possible:
While the above simplification is perfectly valid, it is generally simpler to cancel first and then do the multiplication, since you'll be dealing with smaller numbers that way. In the above example, the 3 in the numerator of the first fraction duplicates a factor of 3 in the denominator of the second fraction, and the 5 in the denominator of the first fraction duplicates a factor of 5 in the numerator of the second fraction. Since anything divided by itself is just 1, we can "cancel out" these common factors (that is, we can ignore these forms of 1) to find a simpler form of the fraction:
This process (cancelling first, then multiplying) works with rational expressions, too.
- Simplify the following expression:
Simplify by cancelling off duplicate factors:
Then the answer is:
Why did you add the "for x not equal to 0" notation after the simplified fraction? Because the original expression was not defined at x = 0 (since this would have caused division by zero in the second of the two original fractions). For the two expressions, the original one and the simplified one, to be "equal" in technical terms, their domains have to be the same; they have to be defined for the same x-values. Since the simplified fraction, 3x/2, has no division-by-zero problem at x = 0, it is not, strictly-speaking, "equal" to the original expression. To make the simplified form truly equal to the original form, you have to explicitly state this "x cannot be zero" exclusion.
- Multiply and simplify the following:
- Multiply and simplify the following expression:
Many students find it helpful to convert the "15" into a fraction. This can make the factors a little more obvious, so one can see more clearly what can cancel with what.
Can you cancel off the 2 into the 20? No! When you have a fraction like this, there are understood parentheses around any sums of terms, like this:
You can only cancel off factors (the entire contents of a set of parentheses); You can NOT cancel terms (part of what is inside a set of parentheses). Barging inside those parentheses, willy-nilly hacking x's and y's and arms and legs off the poor polynomial, doesn't "simplify" anything; it just leaves the sad little polynomial lying there on the floor, quivering and bleeding and oozing and whimpering...
Okay, maybe not; but you get the point: Never reach inside the parentheses and hack off part of the contents. Either you cancel off the entire contents of a parenthetical or factor with a matching parenthetical or factor from the other side of the fraction line, or you do NOT cancel anything at all.
The only thing that you can factor out of the 20x + 25 in the numerator is a 5, and that factor doesn't cancel off with the 2 underneath, so, for this rational, there is no further reduction to be done. Then my final answer is:
Some students, when faced with this problem, will do something like this:
Can they really "cancel" like this? Is this even vaguely legitimate? Has this student done anything at all correctly? No, no, and no!
You can not cancel terms;
you can only cancel factors.
Since you can only cancel factors, my first step in this simplification has to be to factor all the numerators and denominators. Once you've factored everything, you can cancel off any factor that is mirrored on the two sides of the fraction line. The legitimate simplification looks like this:
Can you now cancel off some 2's? Can you cancel off any of the x's with the x2? The x's are only part of their respective factors; they are not stand-alone factors, so they can't cancel off with anything.
The "x not equal to 0, –1 or –3" came from the factors that you cancelled off.
Note: For reasons which will become clear when you are adding rational expressions, it is customary to leave the denominator factored, as shown above. At this stage, your book may or may not want the numerator factored. You should recognize, in any case, that "(2x – 5)(x + 2)2" is the same thing as "2x3 + 3x2 – 12x – 20." http://www.purplemath.com
For further understanding on this lesson, let watch this videos:
To multiply rational algebraic expression:
a.
Write
each numerator and denominator in factored form.
b.
Divide
out any numerator factor with any matching denominator factor.
c.
Multiply
the numerators and also the denominators.
d.
Simplify,
if possible.
Now that you've learned how to multiply rational algebraic expressions, let's do activity 4.
Don't forget to post your answers and for our next meeting review your past lessons on dividing fractions.
Thank you and have a nice day. :)